第19届CPHOS物理竞赛联考已于3月11日结束,共回收试卷902份,有9个省份参赛人数超过40人。经过阅卷、查分环节,我们最终于3月19日公布了最终成绩。本次联考的数据分析已和本文章同步发布。以下是对本次联考的试题评析和答题情况分析。
理论第一题
试题评析
出此题的主要动机是出题人刚刚学完了电动力学,对此部分题目比较熟悉。但是可以发现题目中的大部分内仍然属于普物,即便题目背景很有电动力学的风格,是因为出题人还是尽量避免超纲,将这些知识尽量用普物的方法解决。
本体主要考察考生对最基础的二维无限长的源的电场和磁场的掌握程度,也考察了考生的一定的阅读新概念并应用的能力,本题主要也是围绕着同轴电缆的特性阻抗这个概念展开的讨论。最后一小问也是希望激发考生一定的物理生活应用思维,不仅仅局限在做题的范畴。
本题难度适中,对于水平较高的同学来说应该很容易就秒掉了吧。(这是考前的预测qwq)
作答情况点评
总体来说,第一题的答题情况和我的预期有一定的差距。已经受过更多的竞赛训练的同学本题的发挥比较稳定,基本都能拿到20左右的分数,即将(1)(2)和(3.1)能够基本做对,这也是我对同学们最基本的期望。当然这里(3.2)问损耗功率的计算是本题的唯一难点,确实导致了不少同学的失误,不过略低于预期。
(1)问我是特意限定在了一个二维平面中去考虑问题,就是希望同学们能够运用自己的普物知识而非电动力学来解决,这里其实就是很简单的无限长均匀带电体和无限长均匀直导线的电磁场,只不过要求一下之间的系数比。本题常见错误是写下三维空间的\overrightarrow{E}=-\nabla V, 但是真实情况应该是\overrightarrow{E}=-\nabla V-\frac{\partial\overrightarrow{A}}{\partial t}。所以为了避免引入这种复杂的东西,答案只在二维中求解。本问只求大家不要想太多,简简单单的做完,送分。
(2)问顺势做下来也是送分。
(3.1)问出现了很多共性的问题,首先是这一小问要求要算3个结果,有的人只算了一个P;其次在写出了(11)式后在写出(12)式的时候保留了一些V_0,不知道为啥V_0^2要拆开一个用E_{max}表示了一个却不;最后建议能算数值的时候最后的特性阻抗给出数值。
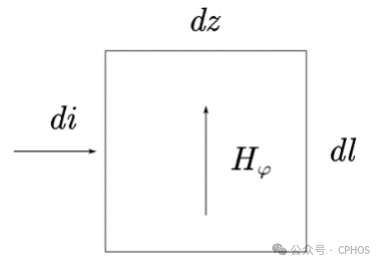
(3.2)稍微解释一下(16)式,这里的R_s说的是单位长度等效的直流电阻,你显然不能理解成R_s=\frac{dR}{dz},因为这样的话R_s就不是导体的性质而是这个波导的性质了,而且内外还一样更奇怪了。我们可以做微元分析,如下图所示:
理论第二题
试题评析
本试题灵感来源于出题人做的一道高数习题,为了给这道题一个物理情景,出题人结合热点事件,出了第(1)问和(2.1)问,并把高数习题放在了第(2.2)问。前面两问可以说是为了平衡试卷难度而故意出简单的,需要选手能一眼看出其难易度并秒杀掉,如果前两问没做对说明基本功不扎实。第(2.2)问就需要一点灵感和运气,需要选手当机立断,有灵感就秒杀,没有灵感就不要死磕。总的来说,本题考察选手的基本功和考试技巧,总体难度小,想拿满有困难。
作答情况点评
本题整体较简单,作答情况相对较好。
本题(1)问较基础,纯几何问题,正确理解题意不难做出,得分率较高;(2.1)问仍是基本的振动问题,需注意分类讨论,最终答案可能有多种等价形式,尽管造成阅卷时较多的误判,但所幸大多予以纠正,本问考察振动的基本功,基础不扎实的同学本问失分较多,基础扎实的同学基本可以拿满分;(2.2)问需要考生灵活应变,以及带有运气成分的些许灵感,跳出传统力学运动学思维,而从数学上考虑问题,本问得分率较低,但类似本问的问题在真正考试中基本不会出现,因此感到有困难也不必担心,本问只是拓展一下大家的思路而已。
理论第三题
试题评析
正如题目开头所言,本题的灵感来源于出题人一次又一次地被洗衣机将卫衣的绳索甩出而折磨(PS:其实只要洗之前绳头打个结就不会甩出来了),因此希望用一个稍微简单一些的模型来模拟绳索被甩出来的过程。连续体的问题是力学模型中的经典,从离散到连续再到微观上的离散,似乎隐隐与物理学几百年的发展过程暗合。由于离心势中连续体的形状分布出题人在查阅了部分文献后,并没有找到解析解[1]。故而采用了简化的模型,使得连续体的形状固定,此时的“连续”仅仅体现在拉力等参数上。
本题的第(1)问在直观上很好解释,摩擦力的存在使得绳索被拉动存在一个阈值。外部绳索足够长则保证了支持力不会反向。其所得到的微分方程是相当经典的一次线性非齐次微分方程,在此考察选手的基本数学功底。
第(2)问的想法同样直观,如果得到了绳索被拉动的阈值,那么绳索被完全抽出的阈值呢?这不可避免地需要研究绳索的动力学,由于拉出过程过于冗杂,不适合在考场上研究,第(2)问是对上述问题的简化,绳索完全抽出的过程过于复杂,在此仅仅着眼于拉动绳索过程中运动。虽然第(2)问的总体思路继承自第(1)问,但是计算量相当大,需要选手相当强的信心和耐心。
作答情况点评
理论第四题
试题评析
出此题的主要动机是笔者选修了一门微电子相关的通识课,该课程主要介绍了集成电路工艺的一些基础知识,如半导体,光电器件,芯片,门电路等。笔者认为这些可作为很好的物理竞赛题目资料。比如本题,是以集成电路中非常重要的原件MOS为背景材料,推导其工作相关的原理,实际上,原意是想在本题之后利用PMOS和NMOS不同的特性引进门电路相关内容,如与非门,再利用门电路设计集成电路版图,达到一个学习原理并应用的效果,碍于篇幅只好割舍,感兴趣的同学可以自行查询资料。
作答情况点评
本题总体而言作答情况不尽人意,一方面说明本题是存在一定难度,另一方面也反映同学们在考场上处理新模型(可能绝大多数同学并未见过此模型)的能力有待提升。实际上,这种题只要能够充分理解题目所给的模型基本就迎刃而解了,即便不能够理解模型的含义,也要从该题涉及的基本物理量,物理学公式出发,紧跟着题目的每一句话的要求,也即它怎么说你怎么写,这样也可以拿到不少分数。尤为重要的是尽量不要跳步,或者在没有完全理解模型,比如只做了第一问就认为第二问和第一问用到的模型一样或差不多,从而直接套用第一问的结论,这样是极有可能错误的。
回归至题目本身,虽然不少同学选择直接跳过,但是做了的同学(1.1)问基本是可以做对。(1.1)问是需要求工作时的外加电压与氧化层、耗尽层之间的关系,而题目直接给出这个关系的即“基于平带状态下施加的额外正电压分成氧化层上的压降V_{ox}和半导体耗尽区压降\varphi_s两部分”,秉持着跟着题目意思走这个原则,讲这句话写成数学表达V_g-V_{fb}=V_{ox}+\varphi_s,则问题转化为分别计算氧化层和耗尽层的压降,求氧化层压降要注意电荷密度的正负号和压降的正向,不过没有注意的话最后两个负号仍然会消掉。(1.2)问注意审题,要给出两种衬底的阈值电压的表达式,(6)式实际就是(5)式的变形,有极少数同学计算时出现了错误,关键是N型衬底这里需要知道它的载流子和P型相反,所以这里我们在平带状态下的加压直接去相反数。
(2.1)问,首先明白此时题目研究的状态“V_g达到阈值电压后继续增加,此时半导体表面电子浓度将超过半导体体内空穴浓度”源区电压为V_s为新加的条件,简记栅极电压为V_{gs},我们可以写出MOS电容结构的反型层电荷密度,注意到是达到阈值电压之后才发生反型的,故自然得到Q_{inv}=-C_{ox}(V_{gs}-V_{th}),又题目告知“当V_b\neq V_s时,反型层电荷面密度Q_{inv}表达式将相比MOS电容结构多了耗尽区单位面积电容C_{dep}在电压V_{sb}作用下的电荷积累,且V_{sb}为正时对反型层电荷贡献为正”可知完整的表达式,将其与原来表达式对比得到等效阈值电压表达式,非常抱歉的是本问最后一句字母提示没有写上V_{sb},但其实原稿上是一个字母提示没有的,当然笔者认为在前面的铺垫下同学们应该知道本题的关键就是V_b\neq V_s,要求的就是这种情况下阈值电压该怎么等效,可想必然答案离不开V_{sb}。(2.2)问开始则进入完整版,考虑源漏端存在压差,即考虑有偏置情况下且考虑偏压对沟道长度的调制作用,看起来很唬人,但还是简单地跟着题目意思去列表达式,无非就是说沟道上的电压与x有关,不再恒等于源电压,那么只需将(2.1)问中的V_s用V_c(x)替换掉即可,如果了解这个模型可知这里的m是体电荷效应的体现,一般仅考虑理想效应时m=1。(2.3)问实际上就是一个积分推导,要注意的是留心会发生饱和,所以是分段函数。并且(2.3)问即便前几问都没有做对,仍然可以拿到(13)(14)(15)式的6分。所以总的来说,这种“新”题属于只要跟着题目走,找到题目中可以转换成数学等式的文字,基于物理学最基础的公式一步步地往下写便可拿到大部分的分数。考场上不可能每个模型都是熟悉的,所以这种能力的训练还是有必要的,可以对照着国际赛和亚洲赛的题目熟悉这种套路。另外,对本题模型感兴趣的同学可以翻阅赵毅强的半导体物理。
理论第五题
试题评析
在我大一上学期的信概课上,一个老师负责讲集成电路部分,他建议我们在写每一期的信概报告时,就自己感兴趣的问题查找相关文献自主学习。我注意到近年光刻机相关技术受到广泛关注,于是自己了解了一下光刻的原理,并将光刻技术中一种较为古老的对准方式出作题目。
本题第(1)问考要求计算相位型光栅的光强分布,考察同学们采用复振幅法计算光强的基本功,思路较为直接;第(2)问与(1)关联不大,题干较长,主要考察同学们读题和理解情境的能力,并试图引导同学们认识该项对准技术的原理。
从另一个眼光看,本题所述模型也可以看作阿贝成像原理的应用。左边透镜对相位光栅进行傅里叶变换并在频谱面上呈现出一系列衍射斑,选取±1级衍射斑相当于只保留相应的低频的信息,这样再经右边透镜的逆变换就在掩膜板上形成原相位光栅的低频像。利用这个像就可以进行对准。实际上,题中由于只用了±1级衍射光,对准精度较低。在目前使用的同类对准方法中,往往利用多级衍射光以提高精度。
在出题人自己理解这一模型的过程中,也遇到一些疑问。比如(2.1)中“将光斑视作新的子波源”,与波在传播过程中的独立性似乎相悖。同时掩膜板上干涉条纹的分布宽度是否就是相位光栅几何光学像的宽度也有待考证。这点留作同学们以及我自己日后详细探究。
作答情况点评
理论第六题
试题评析
1、动机:对于热学熵和相变往往是大家非常忽视的两个部分,但是鉴于39届决赛的不做人所以第6题针对这两个概念进行了考察。
2、考察要点:本题主要是由最基本的热力学定律和熵的基本定义起手,一步步推导出熵的表达式,然后对后面一些问题进行进一步讨论。其考察要点主要是学生是否能掌握简单的偏导(偏微分)应用,以及是否能对热力学中的各个物理量的关系有十分敏锐的感知(个人认为这是热力学解题中最为重要的一环)。
3、命题人胡扯:其实在这个题目实际上来源于我学热学过程中的一些讨论和分析(以及看到北京大雪想到了相变后产生了这个问题)。感觉自己在竞赛阶段对热学的理解非常浅薄,乃至对一些更加基本的概念以及很多热力学关系有相当大的误区,所以希望通过这个题让大家通过最基本的热力学第一定律(或者讲能量守恒)对热学有一个更深刻的认识。而且本题实际是存在一个悖论(paradox)的,我就浅浅把它作为一个彩蛋了欢迎考完这套卷子的家人们battle[2]。
[2] 即全同粒子混合熵变的Gibbs佯谬。
作答情况点评
[3] 有需求的同学也可以参考《物理学大题典》相关章节的问题。
理论第七题
试题评析
作答情况点评
[5] 初版试卷里边不小心把受力写成了f(r)=-\frac{k}{r}!如果正式考试中因审卷不严出现这样的问题,一定要注意根据其余的信息判断这里是否出现失误——倘若真的是f(r)=-\frac{k}{r}形式的力,就不可能出现z(\theta)这种形式的椭圆轨道。虽然这次是我们的笔误,但考生也可以借机学习突发情况的处置方式。
[6] 当然,笔者个人认为正式考试中不会大面积出现这种分析味太重的符号运算。
[7] https://zhuanlan.zhihu.com/p/563486088
[8] https://zhuanlan.zhihu.com/p/342397329
[9] https://arxiv.org/pdf/1909.11659.pdf
[10] V. Arnold, K. Vogtmann, and A. Weinstein, Mathematical Methods of Classical Mechanics. Graduate Texts in Mathematics. Springer New York, 2013.
实验第一题
试题起源
本题基于 “用示波器观测动态磁滞回线”实验,结合交流电路相关基础知识命制。考虑到目前离正式考试尚有数月,本题希望偏重考察考生的基础知识掌握而非实验设计能力与大量数据的处理能力。
命题思路
“用示波器观测动态磁滞回线”不属于《指导书》上的标准实验,实际作答情况也表明本实验对较多考生略显超纲。但笔者认为,无论在理论储备还是实验技术上,考生都应该掌握相关的知识,这一点会结合题目具体分析进行解释。
A1部分提供了较短的一则阅读材料介绍磁滞回线,之后考察了关于磁性材料的基础知识,以及涡流损耗的简化模型。1.1问考察了对物理学常识的基本了解,大部分考生都完成得不太理想。类似的知识还有常见材料的电阻率区间、常见二极管的大致伏安性质等,建议同学们稍加总结、归纳、记忆。
A2部分主要考察考生对交流电相关的实验技术的掌握。本实验看似所用元件较多,但其实回路并不复杂,只是考纲内的简单电路结构的叠加。所涉及到的知识如下:
a.RC积分电路。其实该部分只是RC简单串联,考生需要关注其理论原理,以及实现积分功能所需的近似条件。
b.双踪示波器的测量与接地。有部分考生将“CH1”像电流表一样串联在电路中,暴露出对基础仪器的极不熟练。“示波器信号源需要共地”应该已经是大家的肌肉记忆,但本题的作答情况反映出很多考生并不清楚其根本原因。
c.容/感抗的隔直通交/隔交通直功能。很多考生对交流电路的理解都基于定量的微分方程,但在实验中,对元件的“定性认知”也十分重要:A2.2并不需要大家列出微分方程去逐项分析,应该凭借基础直觉判断出电感的作用。
A3部分是数据处理与误差分析的练习。A3.1需要考生熟悉电磁感应的相关模型,并在紧张状态下正确处理物理量的乘除关系以及公式系数。A3.2要求考生计算一种陌生测量工具的不确定度,但抛去“线宽”“示波器量程=屏幕宽度*分度”的表面,其内核与一般的数字电压表误差公式是完全相同的。
实验第二题
试题评析
本题起源于命题人曾经做到的机构题以及超声光栅的有关实验,数据改编自国际赛题。
作答情况点评
B.1和B.2是传统的超声光栅测声速实验,数据是命题人自己测的,主要考察分光计的基础知识,实验的基本原理,并简要改编了几个大学实验教材中出现的思考题,由于笔试实验考试形式下,许多考生可能没有经历过实验操作,因此需要通过这些思考题训练对实验现象(包括一些“疑难杂症”,即某些情况下仪器状态没有达到测量要求时,表现出的特殊现象以及处理方法)的分析能力,当然命题人还是建议考生进行一些实操训练。
B.3到B.5是比较新的实验形式(但是现在似乎也不新了,机构卷中出现这类实验变多了),需要考生在考场上理解原理,数据来自国际赛题。这部分着重考察了考生的数据处理能力和实验直觉以及估算能力。不少题目要求估算实验参数的量级以及量级不合适的影响,这类题目需要考生具备一定的实验经验,有较好的实验直觉以及估算能力。
作答情况
本题整体得分偏低,理解本题的考生有的接近满分(虽然命题人感觉考场上理解很困难,多半是考生以前接触过类似的题目),未能理解的在10分以下。本题难度其实并不大,细心计算可以获得可观的分数,但不得不承认量太大,需要考生作出合理的时间分配。对于本题实验感到陌生的同学可以去看看国际赛题拓展视野,也可以刷刷机构的实验试卷,以及多看看大学实验教材,在笔试实验的形式下,试题量大,阅读量多的情况已不可避免,赛场上的实验比试更多地依赖于考生的策略和时间分配,建议考生在平时训练自己对试题难度的判断能力和对时间的分配能力。
完整试题及答案下载请访问:第19届CPHOS物理竞赛联考 – CPHOS
文案 | CPHO-S 理论研讨组
CPHO-S 实验研讨组
排版 | CPHO-S 宣传联络组
